Mathematics Awareness Month 2014: Mathematics, Magic, and Mystery
Navigate the Calendar
Myths and Mysteries of the Golden Ratio
No number has been more widely attributed with magical and mysterious properties than the golden ratio. Here to sort out the myths from the even more amazing facts is Stanford mathematician Keith Devlin. In order to get at the central ideas, he includes a careful description of the Fibonacci numbers.
Devlin points out that the design of the video is a parody of some of the truly awful websites that cover the Golden Ratio. The unusual aspect ratio is to stay as far away as possible from 1.6, so no one is tempted to embed the video and put a red “golden rectangle” around it.
Taking it Further
The Golden Ratio is truly a magical number, showing up in many surprising places:
- Consider the number below. It continues in this same pattern of 1s and square roots forever. With a little algebra you can show this number is φ.
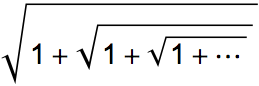
- Here is an interesting sum of fractions, it also continues forever and is also equal to φ. Can you show this continued fraction is equal to φ?
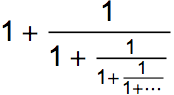
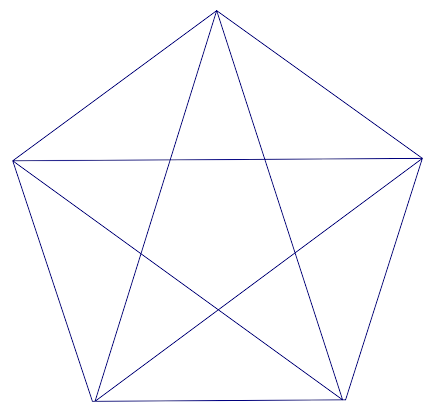
- Get out your ruler and measure the lengths of the line segments in this pentagram inscribed in a regular pentagon. Can you find two different golden triangles (triangles whose side length to base ratio is φ)? Can you prove these ratios are φ?
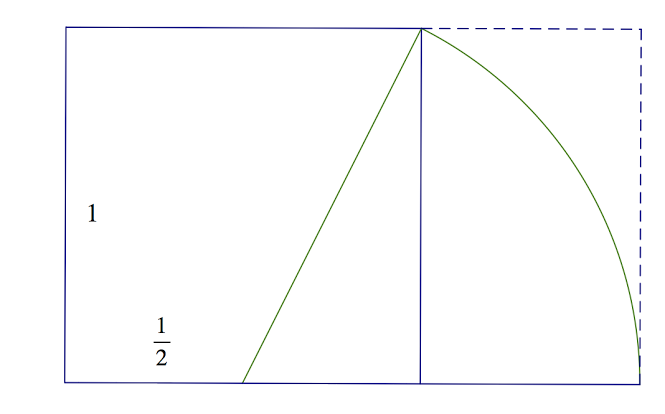
- You can draw a golden rectangle, that is, a rectangle with side lengths 1 and φ, using just a compass and straight edge. The picture below gives a hint. Once you’ve drawn the picture can you prove it is a golden rectangle?
Vi Hart produced a three-part series of videos that provides a lovely exposition on the Fibonacci numbers, the golden ratio, and the evolutionary strategies devised by various plants that tap into these mathematical ideas:
The next time you get the chance, study a pinecone, sunflower, or artichoke, and count the spirals (like Vi does in her first video above). Do you find Fibonacci numbers?
The Underlying Mathematics
A good starting place to learn more about the magical mathematical properties of the the golden ratio is Martin Gardner’s The Second Book of Mathematical Puzzles and Diversions (Simon and Schuster, 1961), currently available as part of the CD compilation Martin Gardner’s Mathematical Games: The Entire Collection of His Scientific American Columns on one CD (MAA, 2008). See Chapter 8, “Phi: The Golden Ratio.”
Are you a fan of all things Fibonacci? Then you should keep an eye out for the Fibonacci Association and the events and conferences they sponsor. For example, they publish The Fibonacci Quarterly, a journal dedicated to mathematics related to the Fibonacci sequence. The journal has been in print since 1963, and back issues up to 2003 may be downloaded for free!