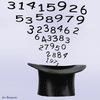Mathematics Awareness Month 2014: Mathematics, Magic, and Mystery
Navigate the Calendar
Does the Declaration of Independence Guarantee Happiness?
Let’s begin this quest for happiness with a card trick. The trick was devised by physicist Martin Kruskal in the 1970s, and popularized by Martin Gardner. You can see it performed here by the always entertaining James Grime:
Author and mathematician John Allen Paulos devised the following inspired variation in which he demonstrates that the Declaration of Independence guarantees happiness!
You can try it yourself: Pick any word from the first two lines of the Declaration of Independence (see the excerpt below). Call it your special word. Count the number of letters in it and move forward that number of words to your next special word. For example, if you picked the word course, which has six letters, as your special word, then you would move ahead six words to necessary, which becomes your next special word. It has nine letters, so you would move ahead nine words brings you to your next special word, which. Continue to follow this rule until you can’t go any further. Explain why no matter what word you pick initially, your last special word will be happiness. Does the Declaration guarantee happiness?
Here’s the example.
When in the Course of human events, it becomes necessary for one people to dissolve the political bands which have connected them with another, and to assume among the powers of the earth, the separate and equal station to which the Laws of Nature and of Nature’s God entitle them, a decent respect to the opinions of mankind requires that they should declare the causes which impel them to the separation. We hold these truths to be self-evident, that all men are created equal, that they are endowed by their Creator with certain unalienable Rights, that among these are Life, Liberty and the pursuit of Happiness.
Now you try it with an initial word different from “course” and check that you still end up with “Happiness.” Here’s the passage again:
When in the Course of human events, it becomes necessary for one people to dissolve the political bands which have connected them with another, and to assume among the powers of the earth, the separate and equal station to which the Laws of Nature and of Nature’s God entitle them, a decent respect to the opinions of mankind requires that they should declare the causes which impel them to the separation. We hold these truths to be self-evident, that all men are created equal, that they are endowed by their Creator with certain unalienable Rights, that among these are Life, Liberty and the pursuit of Happiness.
Taking it Further
Do you see how the card trick works? The magician simply picks a card at random from near the start of the deck and does his own Kruscal count. It is highly likely that your last key card and his will agree! Here are some questions to think about:
- Locate a short passage that appeals to you and see if you can find a common destination that seems to have some significance.
- Can you modify the trick by devising more complicated rules that also lead to a lockstep progression with a common destination?
- In the card trick, two players are not guaranteed to land on the same final card; with a fair deck of 52 cards it is very likely, but not guaranteed. What is the probability that two players, each choosing a random number from 1 - 10 to get started, end on the same final card?
- Can you improve the chances of success by adjusting the value of the face cards from 5 to some other value?
The Underlying Mathematics
The mathematics behind the trick takes some effort to master. Let’s focus on the card trick played on a deck of 52 cards, where the initial key card is randomly selected by the subject from the first 10 cards. The basic idea is quite simple, and is nicely outlined in Paulos’ video above. One way to think about it is to imagine the complete set of key cards that are determined by that initial key card chosen by the subject. The only way for the trick to fail is if when the magician makes his initial selection of a key card, every one of the subject’s key cards are missed by the ensuing progression of the magician’s key cards. If ever the two paths meet, they will continue in lockstep to the same final key card. It is very likely (with probability about 84%) that this will happen.
There is an online version of the card trick that will allow you to explore it efficiently. Pick a card at random from among the first 10 in the top row, and proceed through the deck via Kruskal’s count, reading left to right across the rows. With high probability, your last key card will be the one displayed. The online version is here.
A focused investigation of the trick will require results from the theory of probability. More specifically, a study of Markov chains is required. With an understanding of Markov chains, there is a nice online paper by Wayne Haga and Sinai Robins titled On Kruskal’s Principle that gives all the details. Another good reference is the paper of Lagarias, Rains, and Vanderbei titled The Kruskal Count, from The Mathematics of Preference, Choice and Order. Essays in Honor of Peter J. Fishburn (Springer-Verlag, 2009). James Grime prepared a slightly less advanced synopsis that is available here.
Colm Mulcahy, in his Card Colm from Dec. 24, 2012, gives a slightly simpler version of the card trick. He also provides a very clear heuristic argument to calculate the probability that the simpler trick will succeed. The argument does not require Markov chains. Mulcahy also makes the curious observation that “Outranks luck” is an anagram of “Kruskal count.”
Kruskal’s card trick is described in chapter 19 of Martin Gardner’s book Penrose Tiles to Trapdoor Ciphers (W.H. Freeman, 1989). See page 274 of the 1997 M.A.A. edition. Gardner first introduced the trick to a mathematical audience in his Mathematical Games column in Scientific American (Feb. 1978).
John Allen Paulos first described the application of Kruskal’s principle to passages of texts rather than cards in his book Once Upon a Number (Basic Books, 1999). The relevant excerpt can be found here.
Martin Gardner, in his book Penrose Tiles to Trapdoor Ciphers, makes the following interesting observation:
Rereading “The Disappearance of Lady Frances Carfax,” a Sherlock Holmes tale in the book His Last Bow, I was startled to encounter a remark of Holmes that seems to anticipate the Kruskal count: “When you follow two separate chains of thought, Watson, you will find some point of intersection which should approximate to the truth.”