From SIAM News, Volume 37, Number 3, April 2004

The Structure of Biological and Social Systems

By Guido Caldarelli

Network organization is just about universal in the real world, as evidenced by a consideration of systems as different as the Internet, the World Wide Web, protein interactions, and some financial structures. Such universality is related to the very general nature of network structures. We can take any set of subunits that interact (or communicate) with one another and define a suitable network for the system.

The mathematical description of networks is given by graph theory, which has been used to obtain many analytical results. In general, we can think of the simplest possible graph as a system in which no particular reason is given for drawing a particular link. This, in fact, is the first assumption in the classical random graph theory of Erdös and Rényi. Their model assumes that each pair of vertices is connected randomly with probability p. The result is a structure whose degree (i.e., number of edges per vertex) follows a binomial distribution.

Interestingly, very different behavior is seen in data collected from real-world networks. Here, the degree distribution P(k) decays for large values of the degree k at a much lower rate than in random graphs. For such systems, which are described as "scale-free networks," P(k) follows a power law: P(k) is proportional to k^-γ. Visual inspection shows scale-free networks to be characterized by a few highly connected nodes (hubs) that link the rest of the nodes to the system.

The question that now arises is, What is the reason for this strong deviation from the random case? A-László Barabási and R. Albert have provided one explanation. They explain such an effect by means of a suitable variation of the concept of multiplicative noise. In particular, they assume that the number of vertices in a structure grows constantly. New vertices link to the system through existing vertices that have large degree. These two effects -- growth and preferential attachment -- produce a scalefree network.

We believe that this is only one of the various mechanisms that produce power laws. In some situations neither growth nor preferential attachment occurs, but the resulting graph is still a scale-free network. We consider the main ingredient to be the intrinsic variety and randomness of the different vertices. We assign to any vertex i a particular fitness x_i characterizing its peculiarity. The probability that a link will be created between i and j now becomes a function of x_i and x_j. For a large variety of choices of this function, this "random random graph" model (in the sense that the vertices, too, are now randomly distributed) produces scale-free networks.

As a paramount example of the application of such a model, we considered two financial structures for which we believe that the growth effect plays a very limited role. Parts of the portfolios of different companies (for example, those quoted in a stock exchange) consist of shares of other companies. The subset of those traded in the same stock exchange form a network: The vertices are the companies, and an oriented link is drawn only when an organization owns more than 5% of the other. The result, shown in Figure 1, clearly illustrates the presence of hubs in a scale-free network.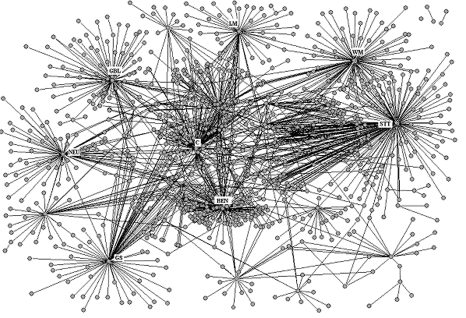

Figure 1. The graph of ownership for stocks traded in 2001 on the New York Stock Exchange.

Another example is given by the characteristic correlation in company stock prices. For any pair of stocks, we can compute the degree of correlation, which induces a metrical distance between the stocks. It is then possible to draw a network of the minimal distance, called the minimal spanning tree of the system (Figure 2). Again, the structure has scale-free properties.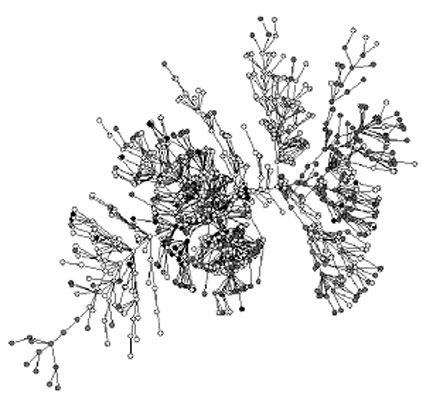

Figure 2. Minimal spanning tree obtained from a large group of stocks traded on the New York Stock Exchange during a 12-year trading period.

Guido Caldarelli is a physicist at the University La Sapienza, Rome.

Download this article as a PDF (812k).