Math Awareness Month - April 2003

Mathematics and Art


Current MAM Home Page || Previous MAWs/MAMs || Current Activities

Here's a neat question that comes from studying the mathematics of art.

Suppose you're watching a baseball game on television, and the screen shows the pitcher getting ready to serve up a fastball to the batter. The pitcher, who is closer to the camera than the batter, takes up a lot more of the TV screen---in fact, he's half again as tall (on the screen) as the batter is. Where on the field is the camera?

This question reverses the one that Renaissance artists had to ask themselves; they knew (or imagined) where their artistic subjects sat in the real world, and so their question lay in how to portray relative sizes on the canvas.

The answer to both questions relies on an old geometric favorite: the similar triangle.

We can think of the television screen (or the easel) as an imaginary wall between the camera (or the eye of the artist) and the baseball players. The pitcher himself becomes one side of a triangle whose opposite vertex is the camera lens; the image of the pitcher on the screen forms the side of a smaller similar triangle. (See the figure below). So we get the equality

The batter, who is about the same height as the pitcher but who stands 60 feet, 6 inches further away, helps to create a second pair of similar triangles---they are similar to each other, but not to the pitcher's triangles. Because we noticed that his image on the TV screen is only two thirds the size of the pitcher's image, we get the second equality,

The reader can check that this gives the distance from the camera to the pitcher of 121 feet. Notice that lots of quantities drop out. What does this say about the physical situation?

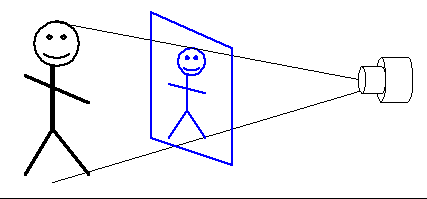
Figure: The baseball pitcher is one side of a triangle whose opposite vertex is the camera lens. The pitcher's image on the screen helps to form a smaller similar triangle.